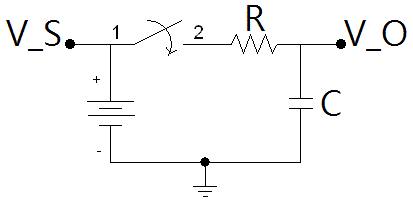
This post explains the math behind a very specific situation: charging a capacitor from 0 V to a fixed voltage through a resistor of known value. The time at which the capacitor begins charging is recent but unknown. By taking two voltage measurements a known amount of time apart while the capacitor is still charging, you can calculate the value of the capacitor.
Motivation
The bus capacitance for I2C is generally specified to be 300 pF maximum. This capacitance does not come from a discrete capacitor but rather from the capacitance of the traces, wires, and cables used to connect devices in the bus. How can we measure this capacitance in-place? Luckily, this bus has a pull-up resistor of a known value. We can use the knowledge of the resistor's value, the I2C voltage we're using, and some math to calculate the bus capacitance.
Derivation
The equation for a charging capacitor is
V_O(t) = V_S*(1-e^(-t/(R*C)))
where V_O is the capacitor's voltage, V_S is the source voltage charging the capacitor, R is the resistor value, C is the capacitor value, and the capacitor is assumed to be initially discharged.
With the substitutions tau=R*C and P=V_O/V_S, we can simplify this equation to
P(t)=1-e^(-t/tau)
Note that P(t) ranges from 0 (the capacitor is fully discharged) to 1 (the capacitor is fully charged).
We can rearrange this to solve for t:
t=-tau*ln(1-P(t))
If we take two measurements along the curve, we now have a system of equations:
t_1=-tau*ln(1-P_1)
t_2=-tau*ln(1-P_2)
where t_1 and t_2 are relative to when we started charging the capacitor and P_1 and P_2 is the capacitor's charged percent at those times. (0 < P_1 < P_2 < 1)
Let delta_t=t_2-t_1 and combine the equations above to get
delta_t=tau*[ln(1-P_1)-ln(1-P_2)]
Solve for C:
C=delta_t/[R*(ln(1-P_1)-ln(1-P_2))]
Photo by Windell Oskay